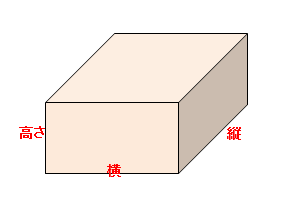
0次元の概念である点、1次元の概念である線、あるいは 2 次元の概念である面の体積は上記の積分による定義では0である。 体積の公式 基本的な体積計算の公式をいくつか示す。( π は円周率) 立方体 s 3 (s は一辺の長さ)立方体の体積は (1辺)×(1辺)×(1辺) で求めることができます。 だけど、これは直方体の (たて)×(よこ)×(高さ) これと全く同じものです。 全ての辺が同じ長さになってしまう立方体では、辺に「2 体積の公式」では,直方体と立方体の体積の求積公式を理解する。立方センチメ-トル(㎤) を単位とすることのよさや,求積公式の意味をしっかりととらえる。さらに「3 大きな体積とか さ」では,1 ㎤より大きな単位に1 ㎥があることを理解し,1 ㎥がどのくらいの大きさなのかとい
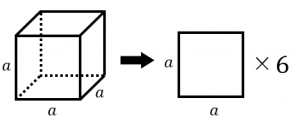
立方体と直方体の表面積を計算する 具体例で学ぶ数学
立方体の体積 公式
立方体の体積 公式-知識・技能 角柱や円柱の体積は、底面積×高さ 直方体や立方体の体積は、既習の公式を用い、 の公式にまとめられることを理解し、8割の児童は求めることができる。三角形の面 基本的な角柱や円柱の体積の計算によ積を求める場面では、2立方体 直方体 体積計算 公式 求め方 縦 横 自動 volume




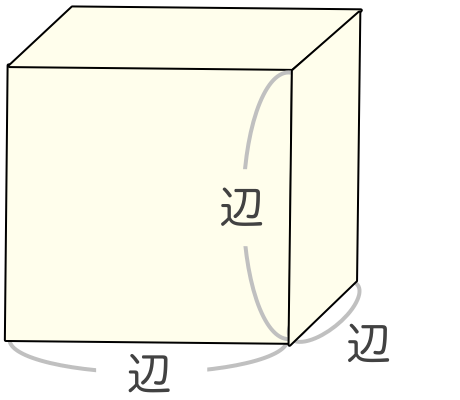
小学算数 立体と体積 直方体 立方体 三角柱 円柱 四角すい 円すい 辺 面 頂点 展開図 体積と表面積の公式 学習ポスター クイズテスト やってみよう ちびむすマンスリー 学習ポスター テストクイズ 3ステップ学習 算数 表面積 小学校 算数
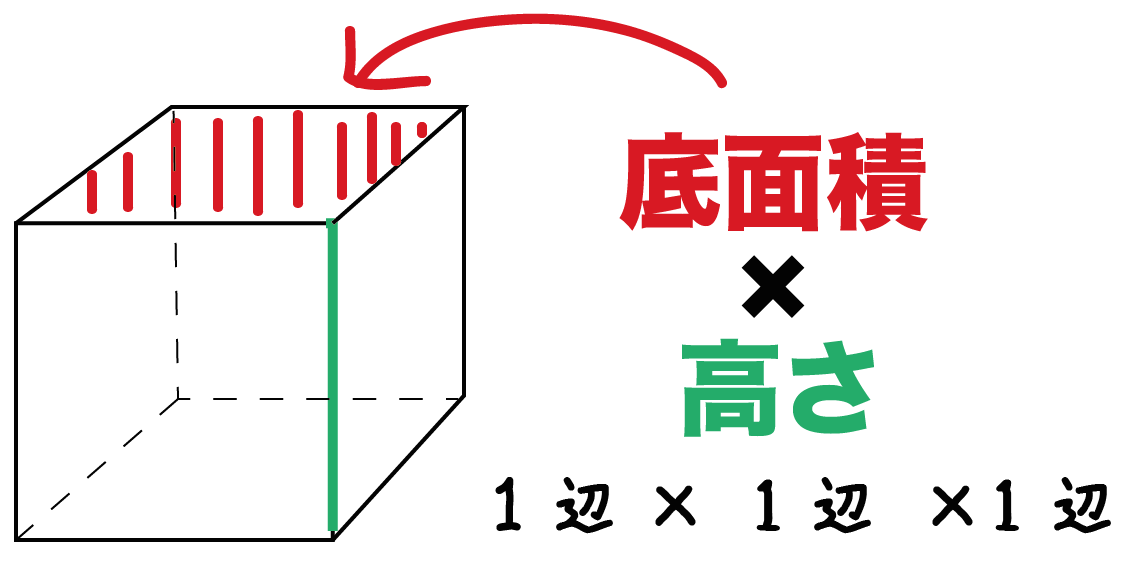
つまり、立方体は全部の辺の長さが同じなので、立方体の体積を求める公式は次のようになります。 「一辺」×「一辺」×「一辺」=体積 一つの辺の長さを3回かける と覚えるとおぼえやすいですね。直方体,立方体の場合の体積の求め方をもとにして,これらの立体の体積も計算によって求める ことができることを理解することが主なねらいとなっている。 本単元では,求積公式を覚えて体積を求められればよいのではなく,どのように考えて公式を導 43 き出していくのかをしっかり理解めあて 公式を使って直方体と立方体の体積を求めよう。 (3)ワークシートの「直方体や立方体の体積の公式」を完成させましょう。 (4)ワークシートの①②③④の体積を計算でもとめましょう。
立方体の体積 立方体の辺の長さ 直方体の体積 四面体の体積 正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から)立方体・直方体の体積の公式 長方形が積み上がってできた\(6\)つの面からなる立体図形を 『直方体』 と言い、すべての辺の長さが同じで\(6\)面がすべて正方形からなる直方体を 『立方体』 と言います。立方体の体積=1辺×1辺×1辺 直方体の体積の求め方公式 直方体の体積は、次の公 小学生・中学生の勉強 算数・数学・国語を中心に小学生・中学生の勉強や夏休みの宿題・おすすめの本について書いています。 直方体の体積の公式を2ステップで解説してみました。求め方がわからない
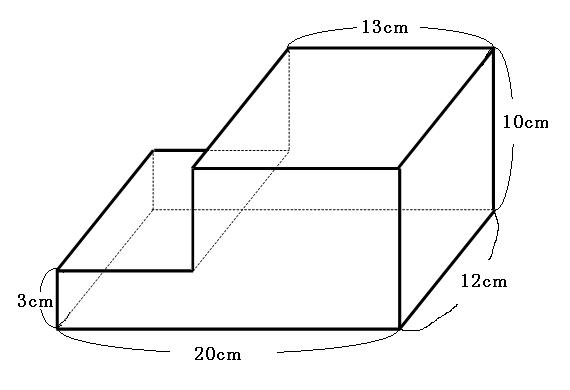
直方体や立方体の体積を求める公式を使って、下の複合図形の体積を求めさせます。 4年生の面積で、複合図形の面積の求め方を思い出させます。 下のアニメは4年のおさらいです 動画作成協力・・動くイラストフリー素材 体積も面積のときのように 2つに分けたり、いろいろなくふうをして立方体の体積を求める公式 体積=辺の長さ×辺の長さ×辺の長さ 辺の長さ3cmの立方体 → 3cm×3cm×3cm → 27cm 3 単位が違う場合の計算方法 立方体の辺の長さ・体積で単位が違う場合は、辺の長さの単位を体積の単位にあわせてから計算をおこないます 辺の長さ300cm、体積?m 3 → 3m×3m×3m → 27m 3の公式でこれを表し ている部分が × になります。 (4)次に(3)の立方体が 段積めるので,右上 の直方体の体積は(1)の大きさの立方体が 個分あるから, cm³ となります。 2 直方体や立方体の体積 学 年 組 氏 名 6cm 6cm 6cm 12m 25m 2m 直方体の体積=たて×横×高さ 4cm 3cm 5cm 2cm 45cm 3cm 3cm 216cm3



Math 積み重ねた立方体の表面積 働きアリ



数学の問題教えてください 立方体から切り取った三角錐の体積はどうやって Yahoo 知恵袋
・体積をはかるもの=1㎤、1㎥の立方体。 ・量を体感する。(実際に実験をすることが大切。) 1㎥に何人ぐらい入ることができるか。自分の家の風呂より大きいか? 1mのものさしで1㎥を作らせると良い。 直方体や立方体の体積の公式。体積公式の帰納法による証明に同じ手法を用いることができる。帰納法の基底段階は 0次元球体と 1次元球体であり、ここで Γ(1) これらは正軸体および超立方体の体積に関する初等的計算と一致する〇体積の単位と単位の相互関係,直方体や立方体の体積の求め方,求積公式の意味を理解している。 知識・理解 5 単元で身に付けたい力を見取る問題と解答例 問題 解答例 ①にしくんがまちがえているところは,内のりの高さの6㎝から2を引いているところです。 ②内のりの高さ



立方体の公式は 1分でわかる意味 体積の公式と例題の求め方 表面積の公式



5年算数体積2わかる教え方
数学切り抜き帳 1辺の長さがaの正四面体の体積はいくらか. この問題は,真っ正直に考えればわかる問題である. じつは,そんなにかた苦しく考えなくても,簡単に答を求める方法がある. 簡単な方法というのは, 「立方体の中に,正四面体が隠れて 半径rの球の体積を求める公式は、次のようになります。 πは円周率(=)です。 球の体積は、半径rの3乗に比例していくということですね! (例題) 半径5cmの球の体積は? 公式 1辺が1cmの立方体の体積が1㎤ です。 今から公式が成り立つ理由を説明する上で重要となりますので、必ず理解をしてください。 立体図形② 直方体の面積「たて×横×高さ」立方体の面積「1辺×1辺×1辺」が成り立つ理由 公式 直方体の体積=たて×横×高さ;




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強
立方体の体積 立方体の辺の長さ 直方体の体積 四面体の体積 正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から)・「体積」の用語を復習する。 1cm 1c㎥ 1cm 1c㎥ 算数科学習指導細案 5年 「体積」 本時の目標 直方体の体積の求め方を考えることができる。 辺の長さを用いることで、直方体や立方体の体積は計算によって求めることが できることを知る。・直方体,立方体の体積の求 め方と公式 ・容積の意味 第6学年 角柱と円柱の体積 ・底面積の意味 ・角柱,円柱の体積の求め方 と公式 面積レ ル3 複合図形 体積レベル3 複合図形 30 2 角柱の体積の求め方を理解する ことができる。 ・四角柱の体積の求め方を基 に,三角柱の体積の求め方 を
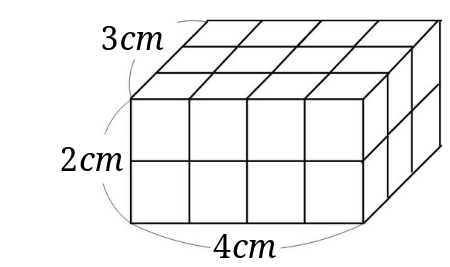



直方体や立方体の体積を求める公式は どうして たて 横 高さ なの みけねこ小学校




立方体や直方体の体積の求め方を習ったら 少し応用的な問題にも取り組みましょう 展開図を見て 体積を求める問題や いくつかの立方体や直方体の面積を足したり引いたりして解く問題です 学習ノート 小学校 算数 学習
立方体の体積の計算問題を解いてみよう それでは、立方体の体積の求め方に慣れるためにも計算問題を解いていきましょう。 ・例題3 1辺の長さが2cmの立方体の体積はいくらでしょうか。 ・解答3 上の立方体の体積の公式を元に計算していきます。化し,直方体と立方体の体積の公式を導いてきた。ま た,図形の面積については,第5学年では四角形と三 角形,第6学年で円について,面積の求め方を学習し てきた。これらの既習事項を活かして,角柱や円柱の 体積公式を導き,計算によって体積を求めることがで きるようにするとともに体積の求め方 そもそも、体積の求め方は、どうやるのか? 小学校で体積を求める方法を習う立体は、立方体と直方体とそれらを組み合わせた立体です。 それぞれの体積の求め方を調べてみると、 直方体:縦×横×高さ 立方体:1辺×1辺×1辺 と書いています。
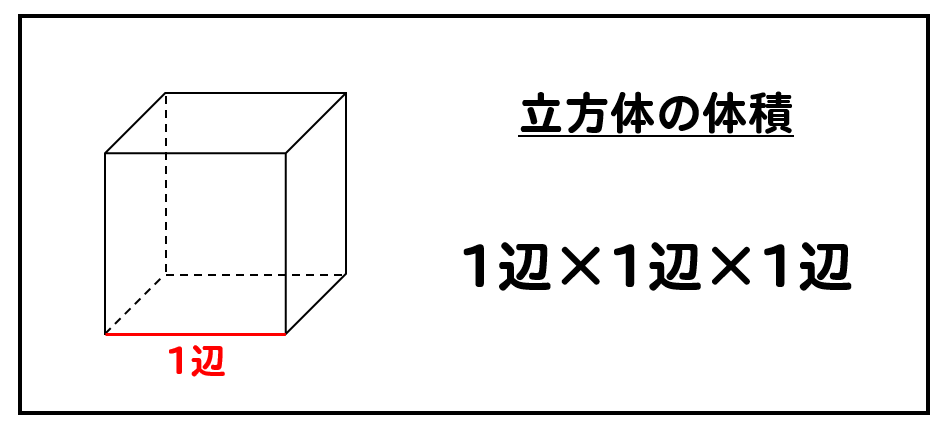



立方体の体積 小学生はどうやって問題解く 計算のやり方を解説 数スタ




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強
立方体の12の辺の長さは等しく、これを $a$ とします。立方体の体積 $V$ は、次の式で求められます。 立方体 (りっぽうたい) の体積 \begin{align*} V = a^3 \end{align*} 体積 = 一辺 × 一辺 × 一辺 立方体の体積の求め方公式 サイコロの形をしている立方体は、一辺の長さがどれも同じ。 立方体の体積は、次の公式で求められます。 立方体の体積=1辺×1辺×1辺 直方体の体積の求め方公式 直方体の体積は、次の公式で求められます。直方体や立方体の求積公式から箱 の体積を求めて,大きさを比べる。 直方体の展開図から,体積を求め る。 式を用いて,体積を求めるこ 直方体や立方体の求積公 とができる。 発言 ノート 3 大 き な 体 積 と か さ Iy 3 Iz 大きな体積を表す単位㎥を知る。 1㎥は何㎤かを考える。 mと㎝で表さ



立方体の公式は 1分でわかる意味 体積の公式と例題の求め方 表面積の公式
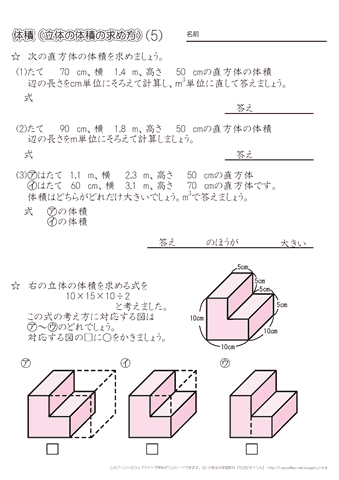



小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生
ってことさ。 たとえば、下の辺が4cm、上の辺が2 cm、高さ6cmの正四角錐台ABCDEFGHがあったとしよう。 この立体の体積は、 1/3 h ( a^2 ab b^2 ) = 1/3 × 6 × ( 4^2 4 × 2 2^2) = 2 × ( 16 8 4 ) = 56 cm^3 になるよ! めんどい計算式だけど、 立方体の体積 立方体の12の辺の長さは等しく、一辺を a とします。 立方体の体積 V は、次の式で求められます。 体積・表面積 算数 中学数学 空間図形 立体の 体積の求め方(公式) を一覧にまとめました。 公式を忘れてしまったときには、こちらで確認しましょう。 体積の求め方公式 立方体・直方体の体積の求め方 円柱の体積の求め方 三角柱の体積の求め




マスラボ 小学校5年 体積 レベル3 立方体の体積の求め方 Youtube
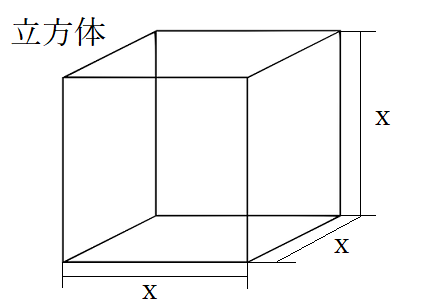



立方体 正六面体 の体積 表面積 計算機 かんたん計算機
長方形が積み上がってできた6つの面からなる立体図形を『直方体』、すべての辺の長さが同じで6面がすべて正方形からなる直方体を『立方体』と言います。 立方体と直方体の体積を求める公式は以下の通りです。 立方体の体積:1辺×1辺×1辺 直方体の体積:縦×横×高さ 直方体の体積は『縦×横』の長方形が『高さ』分だけ積み上がったと考えると、体積は③ 直方体や立方体の体 たいせき 積は,次の公式で求 もと められます。 直方体の体 たいせき 積= × × 立方体の体 たいせき 積= 1 いっぺん 辺 × × ④ 右の直方体の体 たいせき 積を求 もと めましょう。 錐の体積の公式の求め方 ① 立方体を用意する。 そのまんまです。1辺がaの立方体を書いてみましょう。 1辺がaなので、この立方体の体積は、 a×a×a=a 3 ですね。 下の図をイメージしてください。 ② 中心に点を打つ。
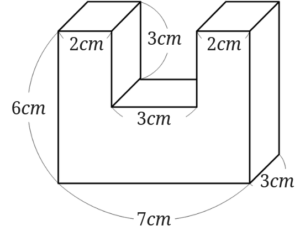



直方体や立方体の体積を求める応用問題の解き方は どうやって教えるといいの みけねこ小学校




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学



立方体の表面積の求め方は 1分でわかる計算 公式 直方体の表面積の求め方
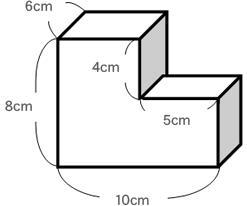



体積 直方体と立方体のかさを表そう 第5学年 小学校 算数 My実践事例 日本文教出版



立方体の公式は 1分でわかる意味 体積の公式と例題の求め方 表面積の公式




無料印刷可能 体積 容積 求め 方



体積計算機 断面積から体積計算 公式 求め方



Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Cc100 Sannsuu Documents S5 023 Pdf



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス




すきるまドリル 小学5年生 算数 体積 無料学習プリント すきるまドリル 無料学習プリント




体積 表面積




中1数学 立体の表面積と体積の求め方と練習問題 Pikuu
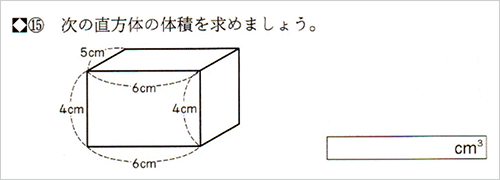



私の実践 私の工夫 算数 直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 啓林館
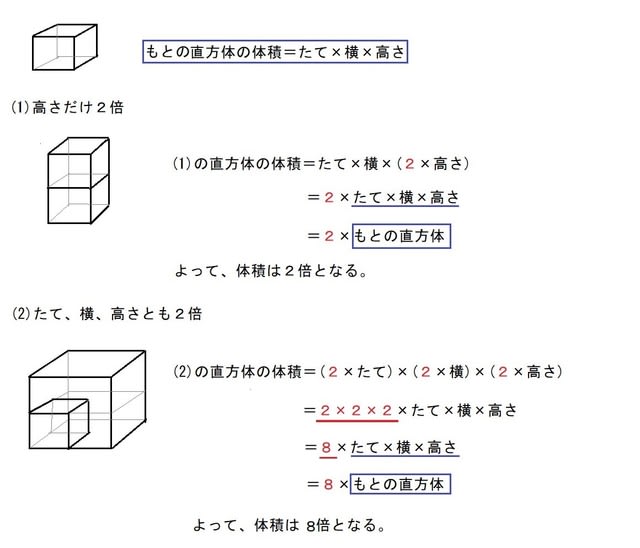



直方体 立方体の体積 小5 きちんと式を書けば簡単 算数の教え方教えますmother S Math Happy Study Support
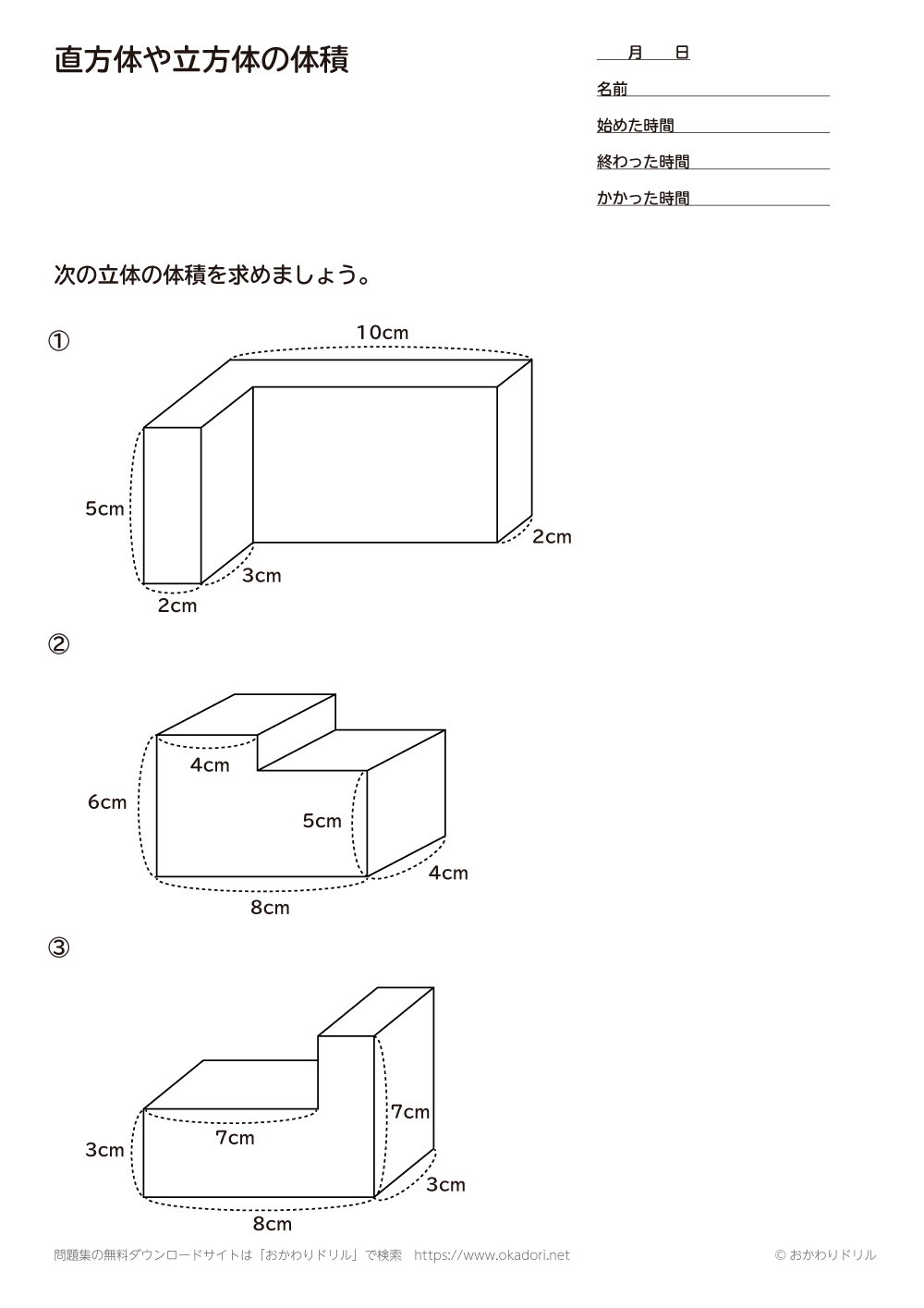



小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル
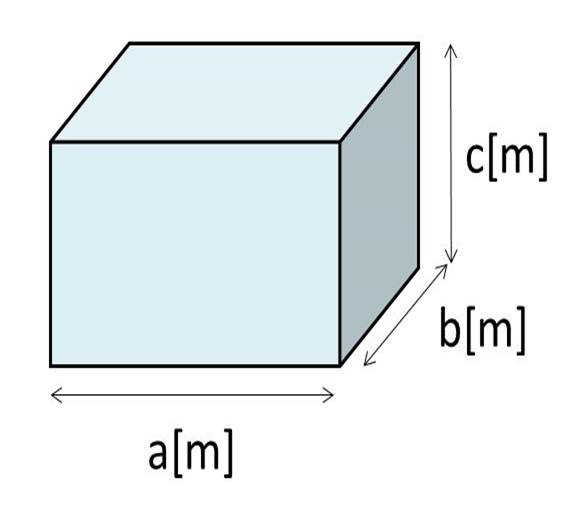



Excel エクセルで立方体 直方体の体積の計算を行う方法 立方メートル 白丸くん




体積の求め方 計算公式一覧



地図の体積計測




計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
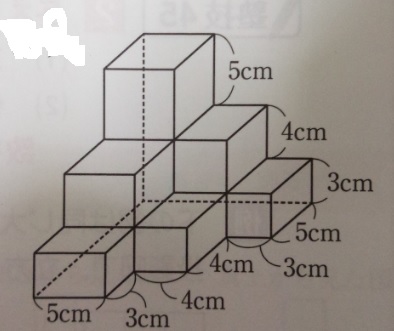



積み重ねられた立体 表面積と体積 中学受験 塾なし の勉強法




多くの教師が失敗する角柱の体積の求め方 算数を究める
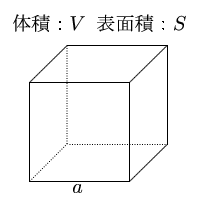



立方体の体積 表面積 体積 表面積の計算 計算サイト
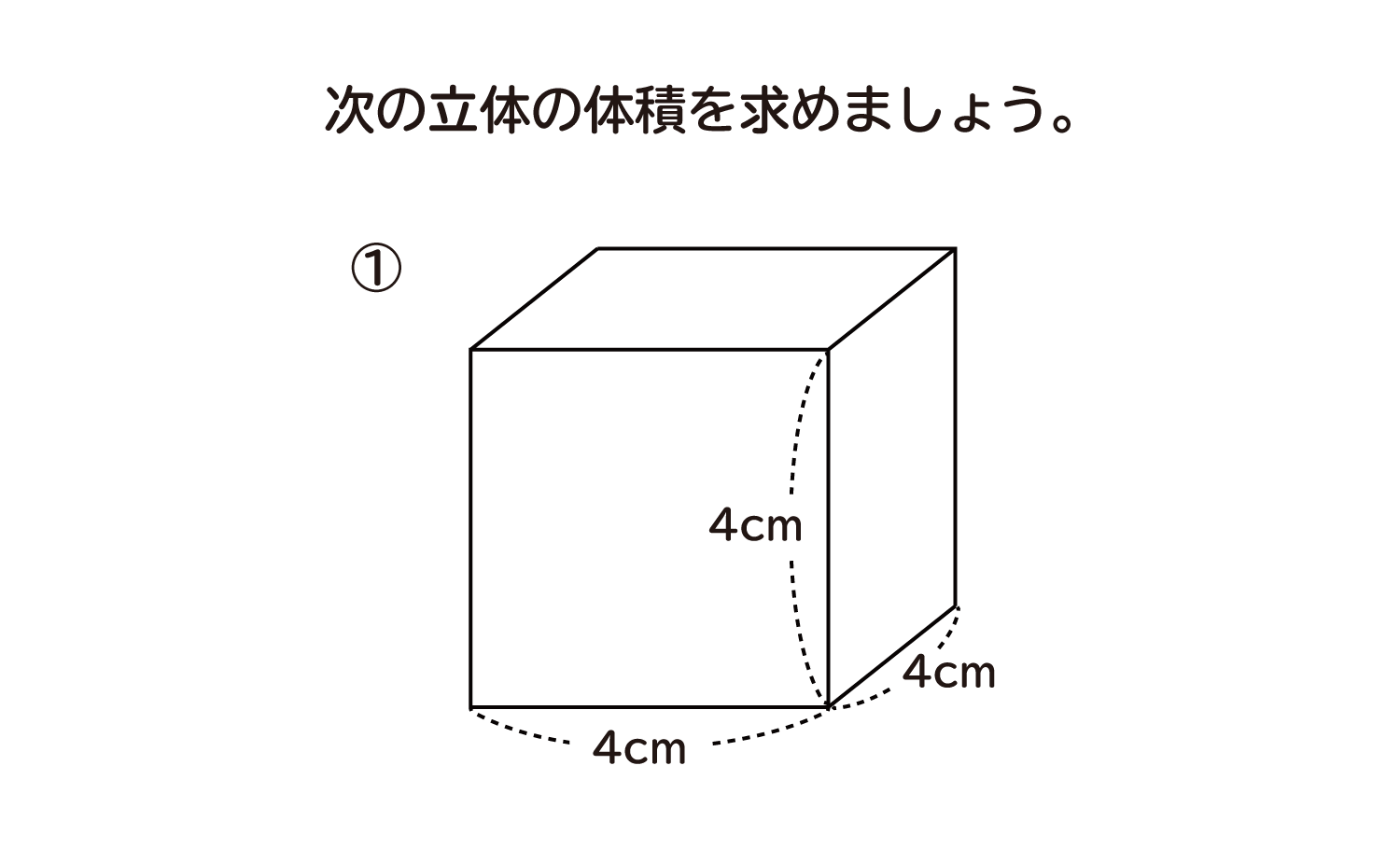



小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル
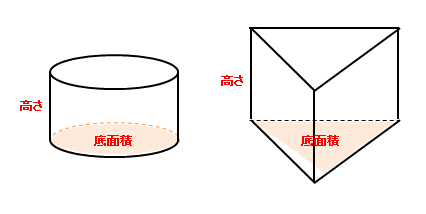



小学算数 立体の体積の公式と単位 立方体 直方体 円柱 三角柱 偏差値40プログラマー



立方体の体積 簡単に計算できる電卓サイト
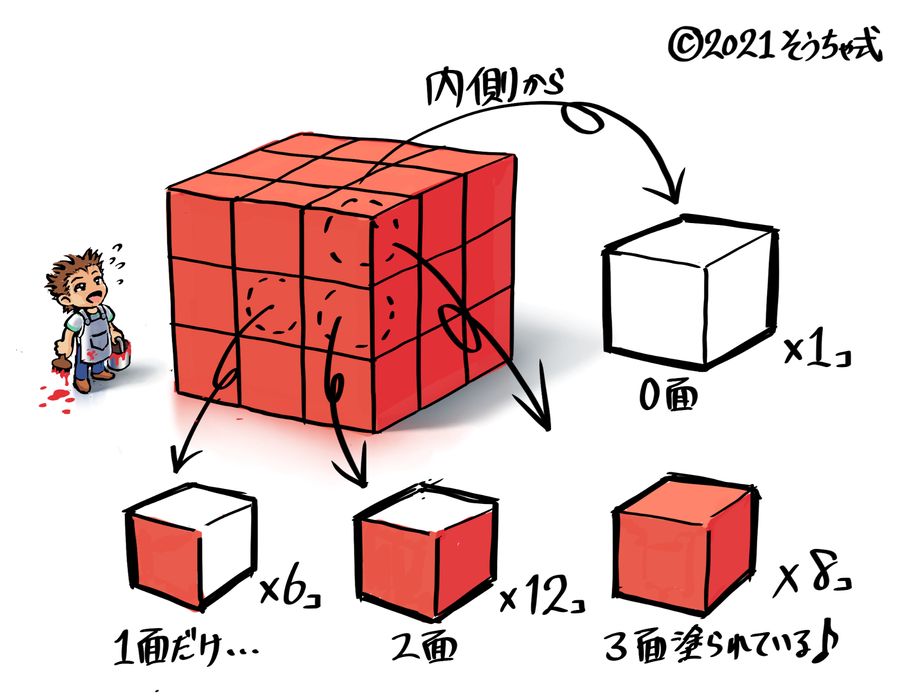



中学受験 直方体 立方体のまとめ 立体図形 そうちゃ式 受験算数 2号館 図形 速さ




立方体の表面積を求める計算と公式 辺と表面積の対応表つき Irohabook




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




どうして1 3なの 錐の体積の公式の求め方 まなべーと




どうして1 3なの 錐の体積の公式の求め方 まなべーと



兵庫県実践事例 算数小学校6年




小5 算数 小5 3 直方体と立方体の体積 Youtube
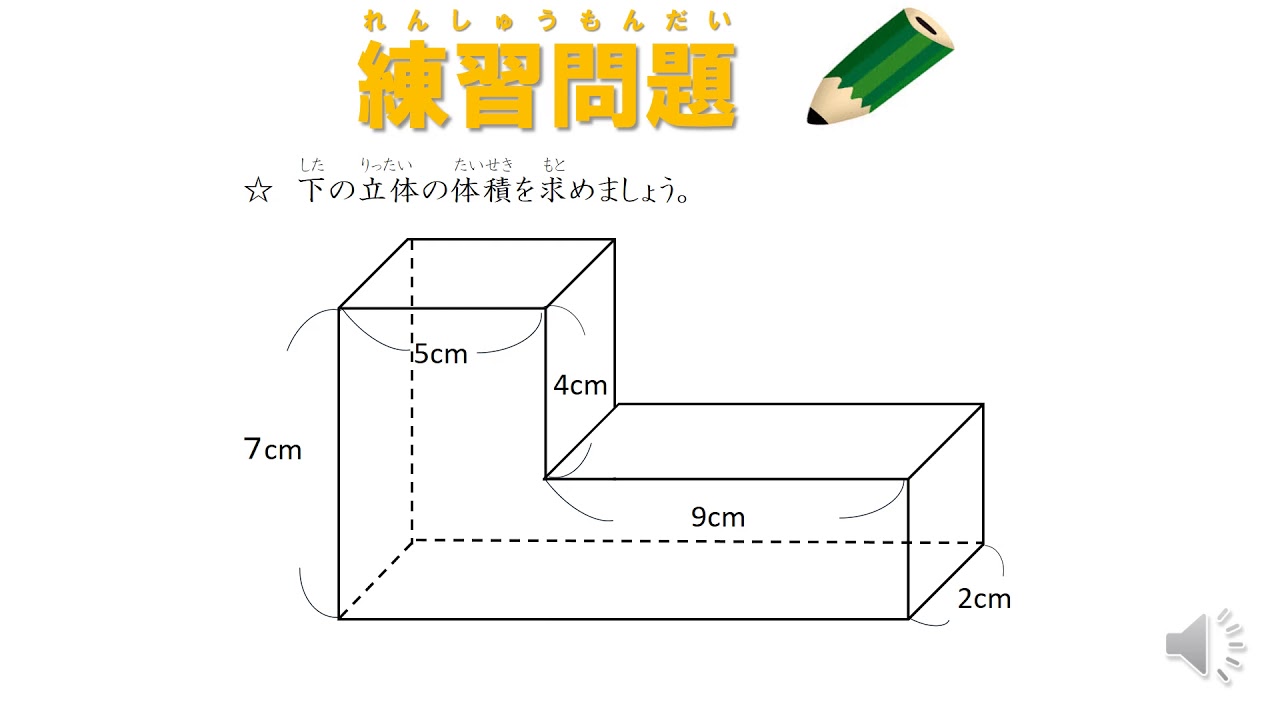



小5 直方体の体積 複雑な立体を求める 日本語版 Youtube




Solids 立体 の英語の名前のまとめ ゆう アメリカ生活終了 英語勉強
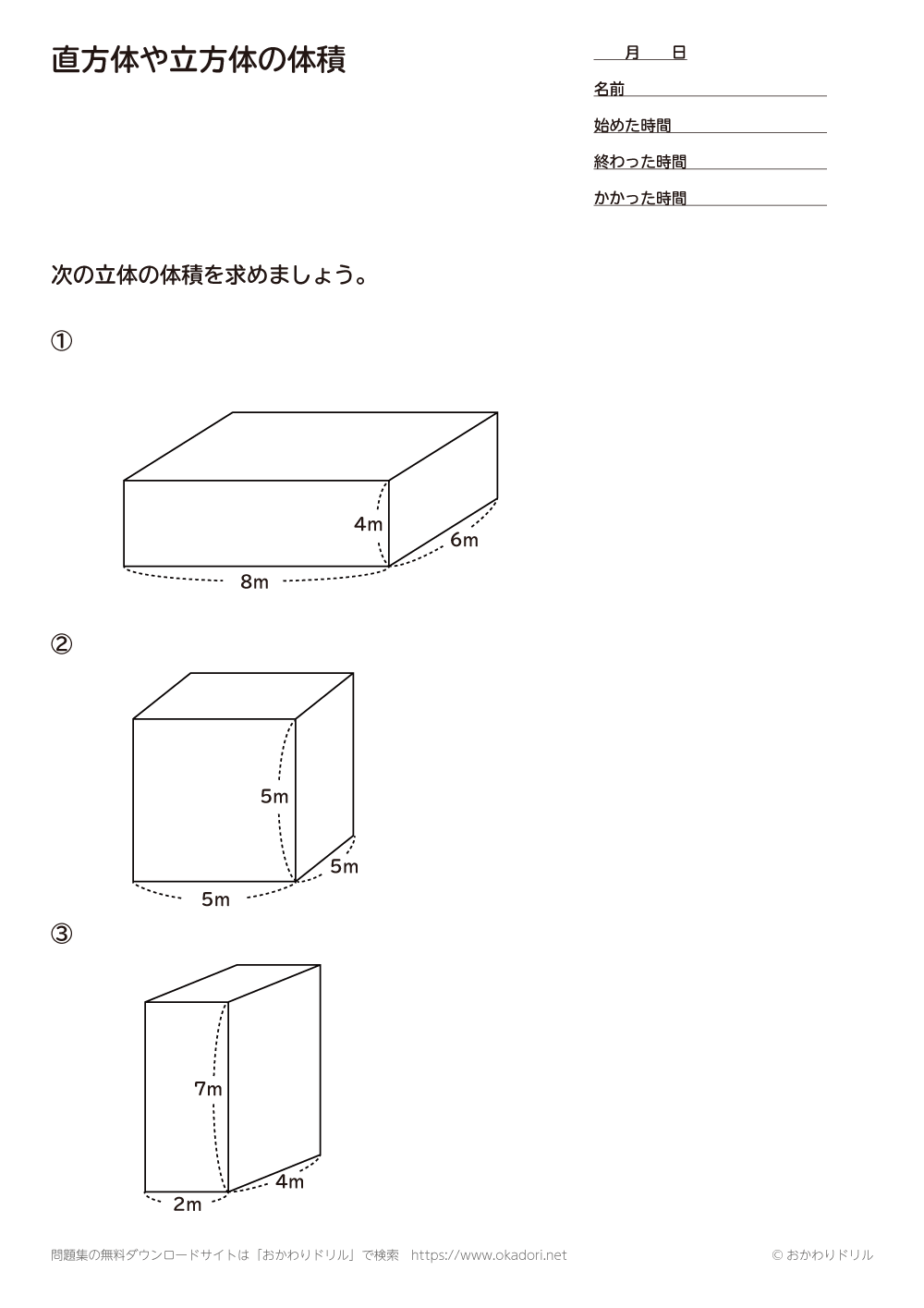



小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル




体積の求め方 計算公式一覧




小学5年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 ちびむすドリル 小学生




立方体と直方体の表面積を計算する 具体例で学ぶ数学
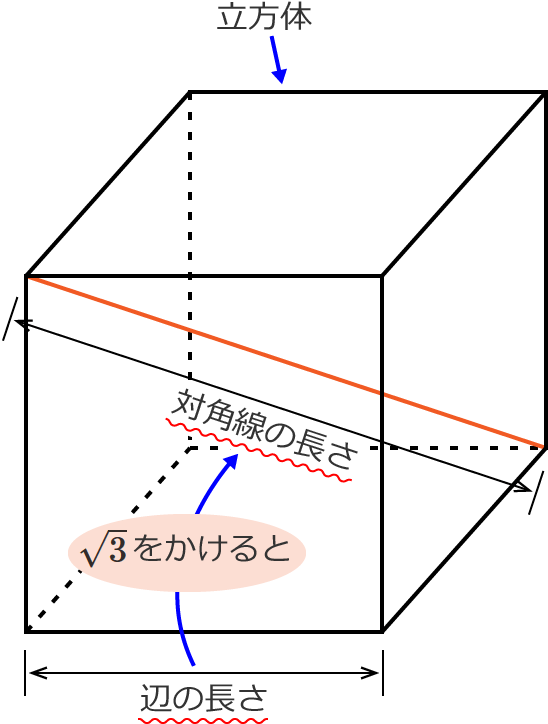



立方体の対角線の長さの求め方




小学算数 立体と体積 直方体 立方体 三角柱 円柱 四角すい 円すい 辺 面 頂点 展開図 体積と表面積の公式 学習ポスター クイズテスト やってみよう ちびむすマンスリー 学習ポスター テストクイズ 3ステップ学習 算数 表面積 小学校 算数




小5 算数 小5 5 体積の求め方のくふう Youtube




体積の測定 測定のことを 即 知りたい ソクシリ キーエンス




スタディピア 立体の体積




直方体 立方体の体積 Youtube



5年算数体積2わかる教え方



立方体 直方体の体積と公式 体積計算機




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット



1




面積や体積のかけ算の順序 おかしな算数教育 身勝手な主張




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強




5年 直方体と立方体の体積 算数イメージ動画集 大日本図書
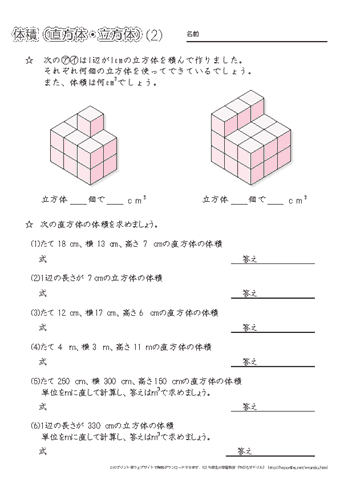



小学5年生の算数 体積 直方体と立方体の体積の求め方 練習プリント ちびむすドリル 小学生



算数流体積の求め方 Sciencelab 冨田塾




複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座




私の実践 私の工夫 算数 直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 啓林館




体積の求め方 計算公式一覧
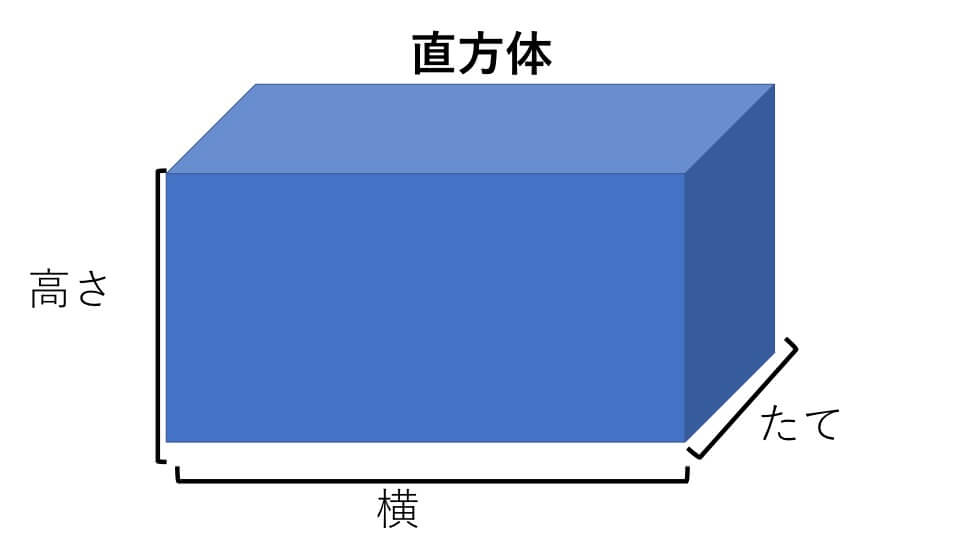



中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー




立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム




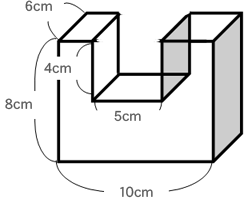



体積 直方体と立方体のかさを表そう 第5学年 小学校 算数 My実践事例 日本文教出版




計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




直方体の体積は 縦 横 高さ じゃなくても求められる ジョン曰く




角柱の体積の公式 求め方は底面積と高さに注目するだけだ 中学や高校の数学の計算問題



小学算数 立体の体積の公式と単位 立方体 直方体 円柱 三角柱 偏差値40プログラマー
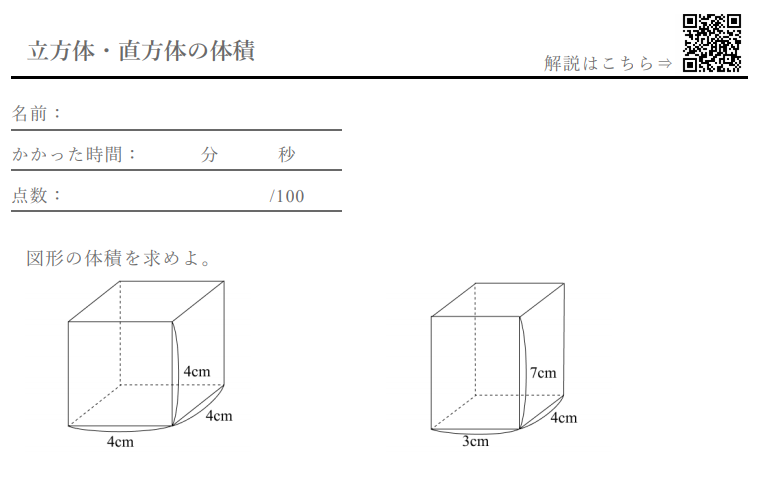



立方体 直方体 の体積 計算ドリル 問題集 数学fun



斜めに切った円柱や角柱の体積を求める方法 中学受験ー算数解き方ポータル



計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




四角錐台の体積 高精度計算サイト



Math 容器にものを入れる問題 公式 体積 底面積 高さ の応用 働きアリ




小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生



1



1




公式を図解 すい体の体積 円すいの表面積の求め方
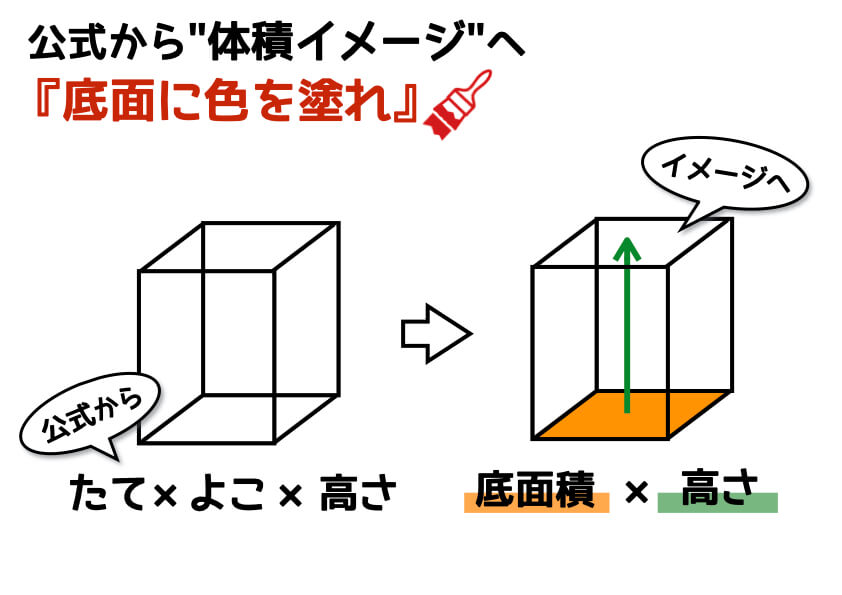



小学生でもスッキリ理解できる 体積比のコツと求め方 中学受験ナビ




立体の体積を求める公式



1
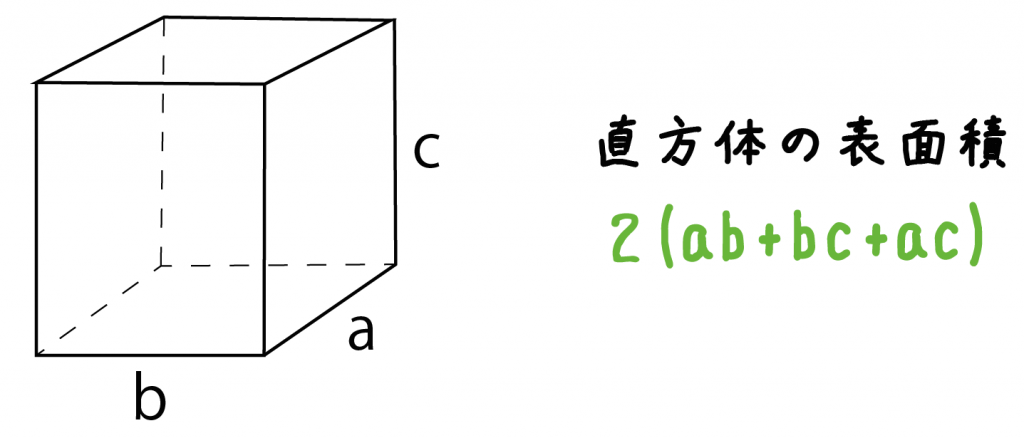



計算公式 直方体の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ
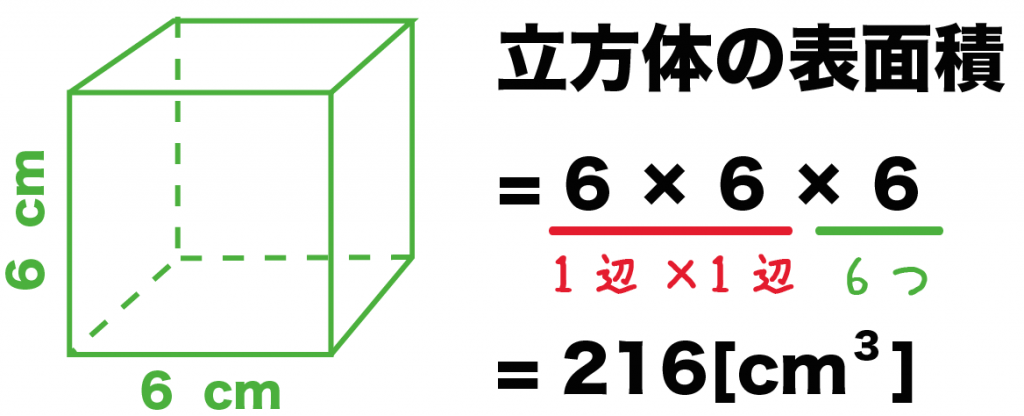



計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun



5年算数体積2わかる教え方




容積の求め方 小学生の算数質問ひろば 進研ゼミ小学講座



5年算数体積2わかる教え方




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー
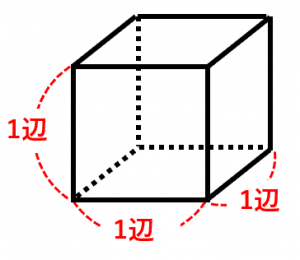



立方体と直方体の体積を計算する方法とツール 具体例で学ぶ数学




体積の求め方 計算公式一覧



わかりやすく 台形の体積の求め方を教えてください わかりやすく 台形の Yahoo 知恵袋



立体の表面積の求め方を解説 面倒な角柱や円柱の表面積をいかにサボって求めるか



0 件のコメント:
コメントを投稿